Our paper, Lattice-Based SNARKs: Publicly Verifiable, Preprocessing, and Recursively Composable, together with Martin R. Albrecht, Valerio Cini, Giulio Malavolta and Sri AravindaKrish-nan Thyagarajan will be presented at CRYPTO’22. There, we build what is suggested in the title based on new families of lattice-based assumptions which we call ![]() -Ring Inhomogeneous Short Integer Solution (k-R-ISIS) and their knowledge variants, k-R-ISIS of Knowledge. These are natural generalisations of the now standard SIS assumption.
-Ring Inhomogeneous Short Integer Solution (k-R-ISIS) and their knowledge variants, k-R-ISIS of Knowledge. These are natural generalisations of the now standard SIS assumption.
Martin has written a gentle introduction of the k-R-ISIS (of Knowledge) assumptions, and Aravind has written about cool things that one could do with our lattice-based SNARKs. In this post, I want to walk you through the construction of our lattice-based SNARKs.
Succinct Non-Interactive Arguments of Knowledge (SNARK)
Succinct non-interactive argument of knowledge (SNARK) allows a prover to convince a verifier about the veracity of statements of an NP-complete language by writing down very short proofs. Our NP-complete language of choice is the satisfiability of systems of quadratic (constant degree in general) equations with bounded coefficients and bounded solutions over certain ring ![]() . More formally, the language is of the form
. More formally, the language is of the form
![]()
where
Vector Commitments (VC)
Instead of building a SNARK, we actually build something even more powerful — a vector commitment (VC) scheme with openings to quadratic polynomials, also known as functional commitments. Such a VC scheme allows the prover to produce a succinct commitment ![]() of
of ![]() , and “open” it to any tuple of quadratic polynomials
, and “open” it to any tuple of quadratic polynomials ![]() by producing a short proof
by producing a short proof ![]() . Given
. Given ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , the verifier could be convinced that indeed whatever
, the verifier could be convinced that indeed whatever ![]() that is committed in
that is committed in ![]() should satisfy
should satisfy ![]() . The tuple
. The tuple ![]() is thus a SNARK proof for
is thus a SNARK proof for ![]() . More on the precise security requirements of the VC later.
. More on the precise security requirements of the VC later.
Basic Construction
In the following, we construct a basic VC which supports openings to a single polynomial ![]() (instead of a tuple).
(instead of a tuple).
Setup
First, a trusted setup generates a random vectors ![]() and
and ![]() over
over ![]() for some modulus
for some modulus ![]() , together with a SIS trapdoor for
, together with a SIS trapdoor for ![]() . Such a trapdoor allows the setup to further generate short vectors
. Such a trapdoor allows the setup to further generate short vectors ![]() over
over ![]() satisfying
satisfying ![]() , for all rational functions
, for all rational functions ![]() for some set
for some set ![]() which will be specified later. The setup then publishes
which will be specified later. The setup then publishes ![]() ,
, ![]() , and the
, and the ![]() ‘s as public parameters.
‘s as public parameters.
Commit
To commit to a short vector ![]() over
over ![]() which has the same dimension as
which has the same dimension as ![]() , the prover simply computes and outputs the inner product
, the prover simply computes and outputs the inner product ![]() .
.
Verify
Before describing the opening algorithm, we first look at the verification algorithm instead. All we need to know about an opening proof ![]() for now is that it is a short vector
for now is that it is a short vector ![]() over
over ![]() which has the same dimension as
which has the same dimension as ![]() .
.
To verify ![]() against
against ![]() , the verifier defines the a quadratic polynomial
, the verifier defines the a quadratic polynomial ![]() as follows:
as follows:
- Parse
 as
as  .
. - Define
 .
.
Then, it checks that are indeed short and satisfy
are indeed short and satisfy  .
.
Open
From the verification equation, we can reverse engineer that the opening proof ![]() should be computed as
should be computed as
![]()
where the rational functions
Weak Binding
We show that the above basic construction satisfies a security notion called weak binding, meaning that it is infeasible for a prover to produce valid opening proofs for ![]() and
and ![]() for
for ![]() , based on the following kRISIS assumption: Given
, based on the following kRISIS assumption: Given ![]() ,
, ![]() , and
, and ![]() generated as in the setup, it is hard to find a short vector
generated as in the setup, it is hard to find a short vector ![]() and a short element
and a short element ![]() satisfying
satisfying ![]() .
.
To see why this is the case, suppose an efficient adversary produces valid opening proofs ![]() satisfying
satisfying ![]() for
for ![]() , by setting
, by setting ![]() and
and ![]() , we have
, we have ![]() . Since
. Since ![]() are short,
are short, ![]() and
and ![]() are also short. We thus have an efficient algorithm for the above kRISIS problem, which we assumed to be hard.
are also short. We thus have an efficient algorithm for the above kRISIS problem, which we assumed to be hard.
From Weak Binding to Extractability
As the name suggests, the weak binding property is weak. In particular, it is insufficient to give a SNARK. What we need instead is extractability, meaning that if a prover is able to produce a valid opening proof of ![]() against
against ![]() , then it is guaranteed that the prover must “know” a satisfying
, then it is guaranteed that the prover must “know” a satisfying ![]() such that
such that ![]() is a commitment of
is a commitment of ![]() and
and ![]() . To achieve extractability, we augment the basic construction as follows.
. To achieve extractability, we augment the basic construction as follows.
- Setup: The setup further generates another random vector
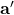 over
over 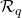 together with its SIS trapdoor, as well as a random element
together with its SIS trapdoor, as well as a random element 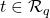 such that the ideal
such that the ideal 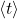 generated by
generated by  has exponentially many elements yet only covers a negligible fraction of
has exponentially many elements yet only covers a negligible fraction of 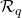 . Using the trapdoor of
. Using the trapdoor of 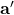 , the setup generates short vectors
, the setup generates short vectors  satisfying
satisfying 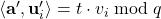 for each entry
for each entry  of
of  . The public parameters now further consist of
. The public parameters now further consist of 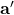 ,
,  , and the
, and the  ‘s.
‘s. - Commit: Unchanged.
- Open: The prover further outputs
 .
. - Verify: The verifier further checks that
 is short and satisfies
is short and satisfies  .
.
We show that the modified construction satisfies extractability based on the following knowledge kRISIS assumption: Given ![]() ,
, ![]() ,
, ![]() , and the
, and the ![]() ‘s generated as in the setup, if an efficient algorithm is able to produce a short vector
‘s generated as in the setup, if an efficient algorithm is able to produce a short vector ![]() satisfying
satisfying ![]() for some
for some ![]() , then the algorithm is guaranteed to “know” a short vector
, then the algorithm is guaranteed to “know” a short vector ![]() such that
such that ![]() .
.
Clearly, by the above knowledge kRISIS assumption, if a prover is able to produce a valid opening proof of ![]() against
against ![]() , then it must know a short vector
, then it must know a short vector ![]() such that
such that ![]() is a commitment of
is a commitment of ![]() . Now suppose that
. Now suppose that ![]() . We can run the opening algorithm to produce a valid opening proof of
. We can run the opening algorithm to produce a valid opening proof of ![]() against
against ![]() . However, this means we can obtain valid opening proofs of
. However, this means we can obtain valid opening proofs of ![]() against both
against both ![]() and
and ![]() , which contradicts weak binding.
, which contradicts weak binding.
Opening to Multiple Polynomials
It remains to further upgrade the construction so as to support opening to not only one but a tuple of polynomials. For this, we further modify our construction as follows.
- Setup: Pick a moderate size modulus
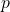 which is small compared to
which is small compared to 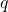 but still large compared to “short” vectors. The public parameters additionally contain a random vector
but still large compared to “short” vectors. The public parameters additionally contain a random vector 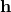 over
over  whose dimension is equal to the number of polynomials to be opened.
whose dimension is equal to the number of polynomials to be opened. - Commit: Unchanged.
- Open: To open to
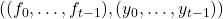 , define
, define 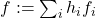 and
and 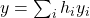 and run the previous opening algorithm to open to
and run the previous opening algorithm to open to 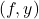 .
. - Verify: To verify an opening proof against
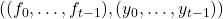 , define
, define 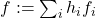 and
and 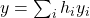 and run the previous verification algorithm to verify
and run the previous verification algorithm to verify 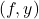 .
.
We show that the third construction remains to be extractable based on the SIS assumption over ![]() . To recall, the SIS assumption states that for a random
. To recall, the SIS assumption states that for a random ![]() it is hard to find a short non-zero vector
it is hard to find a short non-zero vector ![]() such that
such that ![]() .
.
Suppose if a prover is able to produce a valid opening proof of ![]() against
against ![]() . Define
. Define ![]() and
and ![]() . By the extractability of the second scheme, the prover must know a short vector
. By the extractability of the second scheme, the prover must know a short vector ![]() satisfying
satisfying ![]() . Expanding the expression and reducing modulo
. Expanding the expression and reducing modulo ![]() gives
gives ![]() . Note that
. Note that ![]() is short for all
is short for all ![]() . Therefore, if
. Therefore, if ![]() for some
for some ![]() , we obtain a short non-zero vector
, we obtain a short non-zero vector ![]() such that
such that ![]() , violating the SIS assumption.
, violating the SIS assumption.
Last Updated on 21/07/2022.

One thought on “Lattice-based SNARKs from kRISIS of Knowledge”
Comments are closed.