Subtractive Sets over Cyclotomic Rings

This post hopefully makes reading this paper easier.

Motivation

In group-based cryptography, we often find ourselves working over the ring \ZZ_q := \ZZ/q\ZZ where q is most often a prime or a product of a few large primes (in the setting of composite-order groups). Either way, most elements in the ring \ZZ_q are invertible — a fact that is quite convenient for constructing knowledge extractors in \Sigma-protocols and performing polynomial interpolation.

In lattice-based cryptography, however, our playground has been switched to \ring = \ZZ[\zeta_m], the ring of integers of the m-th cyclotomic field, which we call a cyclotomic ring for short. After some experimentation, one can be easily convinced that most elements of \ring are not invertible over \ring, i.e. they are not units. Furthermore, even if we pick a modulus q such that most elements in \ring_q := \ring/q\ring are invertible over \ring_q, the inverses of short elements are often not short. This issue makes many techniques that we take for granted in group-based cryptography inapplicable in the lattice setting.

Subtractive Sets

Long story short, suppose we have a set S \subseteq \ring, which could be the challenge set of a \Sigma-protocol or the set of evaluation points of a Shamir secret sharing scheme. Let T \subseteq_t S be any t-subset of S. It would be great if we can solve the following (dual) Vandermonde systems

    \begin{align*}\mat{V}_T \cdot \vec{z} = s \cdot \vec{w}~\textnormal{and}~\mat{V}_T^\transpose \cdot \vec{z} = s \cdot \vec{w}\end{align*}


over \ring for \vec{z} given some s \in \ring and a vector \vec{w} \in \ring^t. Here, the matrix \mat{V}_T \in \ring^{t \times t} is the Vandermonde matrix defined by the set T. That is, if T = \set{c_i}_{i \in \ZZ_t}, then

    \[\mat{V}_T := \begin{pmatrix} 1 & c_0 & \ldots & c_0^{t-1} \\1 & c_1 & \ldots & c_1^{t-1} \\\vdots & \vdots & \ddots & \vdots \\1 & c_{t-1} & \ldots & c_{t-1}^{t-1} \end{pmatrix}.\]

The element s \in \ring in the above equations, called the slack, is a measure of how good the solution \vec{z} is (if it exists). On one hand, we want (the norm of) s to be as close to 1 as possible. On the other hand, we would like the size n = |S| to be as large as possible since it is inversely-proportional to the soundness error of the \Sigma-protocol using S as a challenge set, and equals to the number of parties to whom we can share our secret. (We might want t to be large for secret sharing as well as it corresponds to the recovery threshold.)

Motivated by the above, we define the notion of (s,t)-subtractive set as a sufficient condition of the solvability of the above (dual) Vandermonde systems. We say that a set S \subseteq \ring is (s,t)-subtractive, if for any t-subset T \subseteq_t S, it holds that s \in \ideal{\prod_{c' \in T\setminus\set{c}} (c - c') } for all c \in T. It is a sufficient condition in the sense that, if a set S \subseteq \ring is (s,t)-subtractive, then any (dual) Vandermonde system defined by the slack s, any target vector \vec{w} \in \ring^t, and any t-subset T \subseteq_t S is solvable over \ring.

Note that in the special case where (c - c') is invertible over \ring for any distinct c, c' \in S, then S is a (1,t)-subtractive set for any 2 \leq t \leq |S|. In this case we simply call S a subtractive set.

Some Math Background and Intuition

In the above definition of (s,t)-subtractive sets, the notation \ideal{x} denotes the ideal generated by the element x \in \ring. That is, \ideal{x} := x\ring := \set{x \cdot r: r \in \ring}. Another way of seeing \ideal{x} is that it contains all the elements in \ring which are divisible by x. So, saying that s \in \ideal{\prod_{c' \in T\setminus\set{c}} (c - c') } is the same as saying that s is divisible by \prod_{c' \in T\setminus\set{c}} (c - c').

Much of the results presented in this work are ultimately due to the presence or absence of certain ideals in \ring. To get a more concrete feeling about the ideals in \ring, the following observation might be useful.

We observe that, over \ZZ, the ring of rational integers, the element 2 is one of the two smallest primes (with the other being -2). Another way of saying this is that 2\ZZ is the “smallest” prime ideal, where the “smallness” is measured by the algebraic norm \mathcal{N}(2) = 2 which measures the number of cosets of 2\ZZ, which is 2. Since 2 is a rational prime, it would be hopeless to find a large (2,t)-subtractive set over \ZZ, since only a handful of elements, \pm 1 and \pm 2, divide 2.

The situation is quite different in \ring = \ZZ[\zeta_m] when m = 2^\ell \geq 4 is a power of 2. There, the ideal \ideal{2} is not prime but actually splits completely into \varphi(m) = 2^{\ell-1} factors. Indeed, we have

    \[2 \in \ideal{2} = \ideal{1 - \zeta_m^{\varphi(m)}} = \ideal{1 - \zeta_m}^{\varphi(m)} \subseteq \ldots \subseteq \ideal{1 - \zeta_m}^2 \subseteq \ideal{1 - \zeta_m}.\]


That is to say, there are quite a lot of elements in \ring that divide 2, which is a good start.

Subtractive Sets over Prime-Power Cyclotomic Rings

Unlike in the paper, we first deal with the easy case. That is to present subtractive sets over prime-power cyclotomic rings, i.e. \ring = \ZZ[\zeta_m] where m = p^\ell is a power of a prime p. These sets S are simply

    \[S = \set{\mu_0, \mu_1, \ldots, \mu_{p-1}}\]


where \mu_k := \frac{\zeta^k_m - 1}{\zeta_m - 1}. Note that S is of size p, and is therefore most interesting when p = \poly and \ell = 1.

Although the proof of the above claim is straightforward, I find it somewhat cute and plausibly insightful. Therefore I decided to include it here.

First, we notice that for 0 < k < p, the element

    \[\mu_k = \frac{\zeta^k_m - 1}{\zeta_m - 1} = 1 + \zeta_m + \ldots + \zeta_m^{k-1}\]


is a unit. Indeed, it is called a cyclotomic unit and its inverse is given by

    \[\sum_{i \in \ZZ_h} \zeta_m^{ik \mod m}\]


where h = k^{-1} \mod m.

Next, we notice that \mu_k can be written as a prefix sum of the sequence of powers of \zeta_m. Consequently, for 0 \leq i < j < p, we have

    \begin{align*}\mu_j - \mu_i &= \zeta_m^i + \zeta_m^{i+1} + \ldots + \zeta_m^{j-1} \\&= \zeta_m^i \cdot (1 + \zeta_m + \ldots + \zeta_m^{j-i+1}) \\&= \zeta_m^i \cdot \mu_{j-i}\end{align*}


which is invertible.

(2,3)-Subtractive Sets over Power-of-2 Cyclotomic Rings

If all the world cares about is prime-power cyclotomic rings, then we would have been done. However, power-of-2 cyclotomic rings are more preferable in implementations due to convenient tools such as the number theoretic transform (NTT). To be clear, these rings are \ring = \ZZ[\zeta_m] where m = 2^\ell \geq 4 is a power of 2.

For the purpose of constructing lattice-based Bulletproof over power-of-2 cyclotomic rings, we are interested in constructing large (s,3)-subtractive sets over \ring. In this blog post, we pick s = 2 as an example, and prove that

    \[S = \set{0,1,\zeta,\zeta^2,\ldots,\zeta^{\varphi(m)-1}}\]


is (2,3)-subtractive. Note that in the above I wrote \zeta for \zeta_m.

First, we note that we get the element 0 in the set for free, since all other elements are units. It therefore suffices to prove that

    \[S' = \set{1,\zeta,\zeta^2,\ldots,\zeta^{\varphi(m)-1}} = S \setminus \set{0}\]


is (2,3)-subtractive. To this end, consider any 3-subset

    \[T = \set{\zeta^a, \zeta^b, \zeta^c} \subseteq S'\]


where we assume without loss of generality that

    \[0 \leq a < b < c < \varphi(m) = 2^{\ell-1}.\]


We want to show that

    \[2 \in \ideal{(\zeta^a - \zeta^b)(\zeta^a - \zeta^c)}.\]

To do this, we first note that

    \[\ideal{(\zeta^a - \zeta^b)(\zeta^a - \zeta^c)} = \ideal{(1 - \zeta^{b-a})(1 - \zeta^{c-a})}\]


since \zeta^{-a} is a unit. Next, by some routine calculation, we can see that

    \[\ideal{(1 - \zeta^{b-a})(1 - \zeta^{c-a})} = \ideal{(1 - \zeta^{\mathrm{Ev}(b-a)})(1 - \zeta^{\mathrm{Ev}(c-a)})}\]


where \mathrm{Ev}(x) denotes the even part of x \in \ZZ, i.e. the largest power of 2 which divides x. To proceed, we perform some more routine calculation to be convinced that

    \begin{align*}\ideal{(1 - \zeta^{\mathrm{Ev}(b-a)})(1 - \zeta^{\mathrm{Ev}(c-a)})} &= \ideal{(1 - \zeta)^{\mathrm{Ev}(b-a)} (1 - \zeta)^{\mathrm{Ev}(c-a)}} \\&= \ideal{(1 - \zeta)^{\mathrm{Ev}(b-a) + \mathrm{Ev}(c-a)}}.\end{align*}


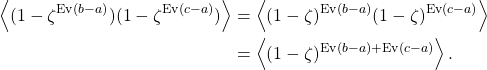
Finally, we observe that \mathrm{Ev}(b-a) + \mathrm{Ev}(c-a)} \leq 2^{\ell-1} and therefore

    \[2 \in \ideal{1-\zeta}^{2^{\ell-1}} \subseteq \ideal{(1 - \zeta)^{\mathrm{Ev}(b-a) + \mathrm{Ev}(c-a)}}.\]

Impossibility of Large (s,t)-Subtractive Sets

We conclude this blog post by showing that one cannot find (s,t)-subtractive sets that are much better than those constructed above.

For the impossibility result, it would be convenient to introduce the notion of weak (s,t)-subtractive sets, which are sets S such that, for any t-subset T \subseteq_t S, it holds that s \in \ideal{T-T}. Here, the set T-T is defined as

    \[T - T := \set{t - t': t,t' \in T}\]


and \ideal{T-T} is the ideal generated by the elements in the set T-T. From the definitions of (weak) (s,t)-subtractive sets, one can immediately see that an (s,t)-subtractive set is also weakly (s,2)-subtractive. Therefore, if we can rule out the existence of certain weakly (s,2)-subtractive sets, we would also be able to rule out the existence of certain (s,t)-subtractive sets.

Power-of-2 Cyclotomic Rings

We first consider power-of-2 cyclotomic rings \ring = \ZZ[\zeta_m] where m = 2^\ell \geq 4 is a power of 2. Suppose that m+1 is a prime (which is called a Fermat prime, with known examples being 5, 17, 257, 65537), then \ideal{m+1} splits into \varphi(m) = 2^{\ell-1} factors each having algebraic norm m+1. That is, each factor \mathcal{I} of \ideal{m+1} has m+1 cosets.

Fix one of these factors \mathcal{I}. Suppose S is a weakly (2,2)-subtractive set of size greater than m+1, we can partition S such that each subset contains elements belonging to the same coset of \mathcal{I}, with one of the subset T \subseteq S containing at least 2 elements by the pigeonhole principle. However, since all elements in T belong to the same coset of \mathcal{I}, we have \ideal{T-T} \subseteq \mathcal{I}. Since S is weakly (2,2)-subtractive, we have 2 \in \ideal{T-T} and hence 2 \in \mathcal{I}. This however is a contradiction because 2 is clearly not in \mathcal{I} (since the latter has norm m+1 which is coprime with 2).

From the above, we conclude that, for any t, it is impossible to construct a family (parameterised by m) of (2,t)-subtractive sets each of size greater than m+1. We note that, however, this result only rules out families of constructions but not individual constructions. That is, it might still happen that there exists a (2,2)-subtractive set of size 1026 in the 1024-th cyclotomic ring.

Prime-Power Cyclotomic Rings

We finish by considering prime-power cyclotomic rings \ring = \ZZ[\zeta_m] where m = p^\ell is a power of a prime p. Here, we notice that the ideal \ideal{1-\zeta_m} has algebraic norm p — it has p cosets — and 1 \notin \ideal{1-\zeta_m}. Thus, by the same argument as above, we can conclude that there is no subtractive set of size greater than p over prime-power cyclotomic rings. In other words, the constructions that we gave above are in a sense optimal.

Last Updated on 11/07/2022.

Leave a Reply

Your email address will not be published. Required fields are marked *